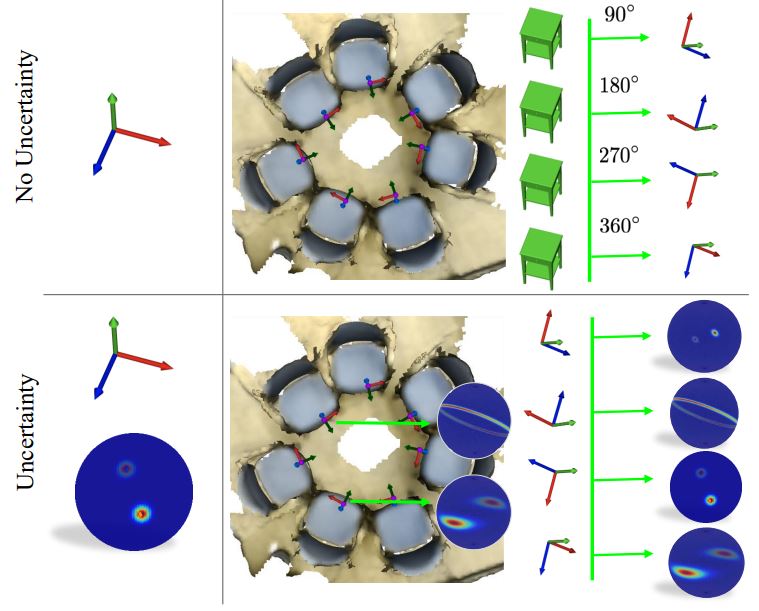
Multi-modal 3D Vision
Investigates the uncertainties and ambiguities in 3D vision problems such as pose estimation, reconstruction and etc.
A majority of tasks in computer vision can be interpreted as scene understanding problems conditioned on either 2D image or 3D scan modalities. Usually, these scenes are digitizations of our man made environments composed of objects. Hence, a fundamental piece of this perception problem is pose estimation, i.e. figuring out how these objects are positioned and oriented in 3D space. A rigid transformation is a six degrees of freedom (6-DoF) entity explaining the pose either of an acquisition device (e.g. Lidar or cam- era) or an object enclosed within the captured data. Solving for the former is known as camera relocalization, while the latter is related to 3D object pose estimation. Both of these are now key technologies in enabling a multitude of applications such as augmented reality, autonomous driving, human computer interaction and robot guidance, thanks to their extensive integration in simultaneous localization and mapping (SLAM) [24, 32, 83], structure from motion (SfM), metrology, visual localization and 3D object detection. A myriad of papers have worked on finding the unique solution to the pose estimation problem: a pose per view/scan. However, this trend is now witnessing a fundamental challenge. A recent school of thought has begun to point out that for our highly complex and ambiguous real environments, obtaining a single solution i.e. the correct pose, is simply not sufficient. For example, an image of a scene with repeating structures can look similar even though the location and orientation of the capture de- vice is drastically different. Likewise, objects with rotational symmetries lead to very similar point clouds when scanned from different viewpoints, say with a laser scanner. These observations have led to a paradigm shift that has opened a multitude of research directions focusing on these issues. In- stead of estimating a single solution, methods now propose to predict a range of solutions providing multiple pose hypotheses, solutions that can associate uncertainties to their predictions or even solutions in the form of full probability distributions.
Related Publications
2020
2022
2024
-
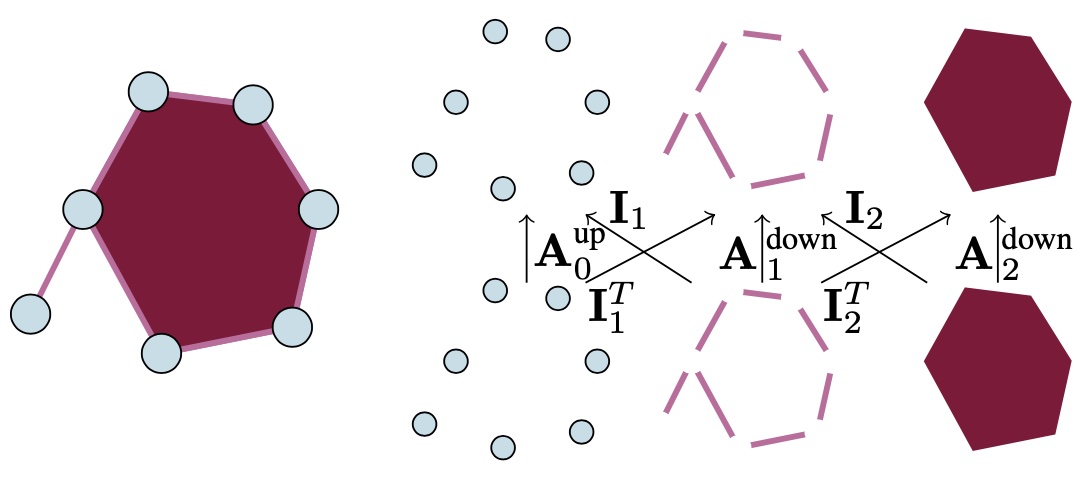 Attending to Topological Spaces: The Cellular TransformerarXiv preprint arXiv:2405.14094, 2024
Attending to Topological Spaces: The Cellular TransformerarXiv preprint arXiv:2405.14094, 2024
2024
-
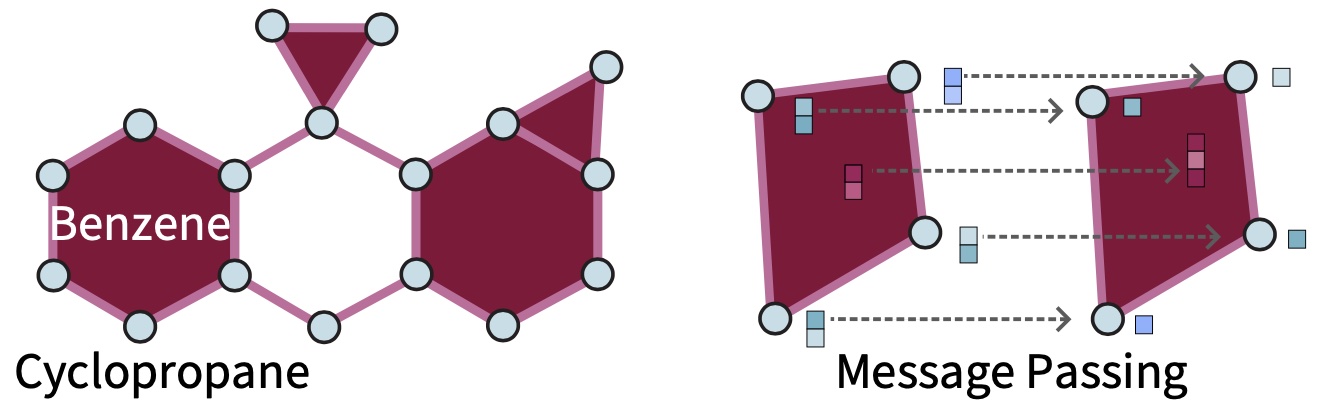 Position: Topological Deep Learning is the New Frontier for Relational LearningIn Int. Conf. Machine Learning (ICML), 2024
Position: Topological Deep Learning is the New Frontier for Relational LearningIn Int. Conf. Machine Learning (ICML), 2024